ဖန်ရှင်
သင်္ချာတွင် ဖှန်ရှင် (အင်္ဂလိပ်: function) သည် ကိန်း (quantity) နှစ်ခု အကြား မှီခို ပြောင်းလည်းမှုကို ဖော်ပြသော အရာဖြစ်ပြီး လွတ်လပ်သော (independent) ကိန်းကို ဖှန်ရှင်၏ အဝင်ကိန်း ဖြစ်ပြီး မှီခိုသော ကိန်းသည် ဖှန်ရှင်၏ အထွက်ကိန်း (output) ဖြစ်သည်။ ဖှန်ရှင်တစ်ခုသည် အဝင်ကိန်း တစ်ခုအတွက် ပုံသေဖြစ်သော အထွက်ကိန်း တစ်စုံ ရှိပြီး မတူညီသော အဝင်ကိန်း သောလည်း တူညီသော အထွက်ကိန်း ရှိနိုင်သည်။ အစုအားဖြင့် ဆိုရသော် ပြောင်းလဲကိန်းများ အစုကို ဒိုမိန်း သို့မဟုတ် အကြောင်းခံဝန်းနယ် (domain) ဟု ခေါ်ပြီး၊ ရလဒ်တန်ဖိုးများ အစုကို ကိုဒိုမိန်း သို့မဟုတ် အကျိုးဆက်ဝန်းနယ် (co-domain) ဟု ခေါ်သည်။[၁][ပိုမိုကောင်းမွန်သော ရင်းမြစ် လိုအပ်သည်] ဤတွင် ဖှန်ရှင်ဟူသည်က အစုX (အကြောင်းခံနယ်ဝန်း)[၂] မှ အစုY (အကျိုးဆက်ဝန်းနယ်)သို့ အစုဝင်များ အချင်းချင်း ဆက်စပ်ပေးသော ဆက်သွယ်ချက်မျိုး ဖြစ်ပေမည်။[၃]

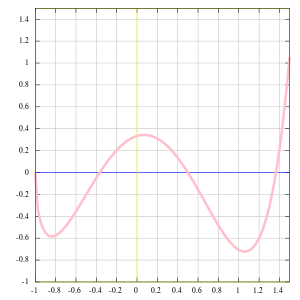
ဖှန်ရှင်တစ်ခုကို ဖော်မြူလာ ဖြင့်သော်လည်းကောင်း၊ ဂရပ်ဖ်ပုံ ဖြင့်သော်လည်းကောင်း၊ တွက်ချက်၍ရသော အယ်လ်ဂေါ်ရီသမ် ဖြင့်သော်လည်းကောင်း ဖော်ပြနိုင်သည်။ အသုံးချ ပညာရပ်များတွင် ဖှန်ရှင်ကိုယ် တန်ဖိုးပြ ဇယားများ ဖြစ်လည်း ဖော်ပြကြသည်။ ဖှန်ရှင်အားလုံးကို ဤနည်းများအားလုံးဖြစ် ပြတော့မဖြစ်နိုင်ပေ။ ထို့အပြင် ဖှန်ရှင်နှင့် ဖန်ရှိကိုဖော်ပြခြင်း သို့မဟုတ် ပုံဖော်ခြင်းမှာ မတူကြောင်း သိရှိရန်လိုပေသည်။
အသုံးများသော ရေးနည်းအားဖြင့် ဖှန်ရှင်များကို ပုံစံဖြင့်ရေးနိုင်ထားလျှင် က သွင်းကိန်း (input) သို့မဟုတ် အမှီခိုခံ ပြောင်းလဲကိန်း (variable) ကို ဆိုလိုပြီး သို့မဟုတ် က မှီခိုသူ ထွက်ပေါ်ရလဒ် (output) ကိုဆိုလိုသည်။ ဖန်ရှင်ခွဲစိတ်ဗေဒ (Functional Analysis)တွင် ထို၂ခုအနက် အနည်းဆုံးတစ်ခုသည် တိုင်းကြောင်း အရေအတွက် (၂ခု၊ ၃ခုသာ မက) အနန္တပင် ရှိနိုင်သည့် ရပ်ဝန်းများ (infinite-dimensional spaces) လည်း သဘောတရားအားဖြင့် ဖြစ်နိုင်သည်။ [၅]
အသုံးများသော ရေးနည်းအားဖြင့် ဖှန်ရှင်များကို ပုံစံဖြင့်ရေးနိုင်ထားလျှင် က သွင်းကိန်း (input) သို့မဟုတ် အမှီခိုခံ ပြောင်းလဲကိန်း (variable) ကို ဆိုလိုပြီး သို့မဟုတ် က မှီခိုသူ ထွက်ပေါ်ရလဒ် (output) ကိုဆိုလိုသည်။ ဖှန်ရှင်ခွဲစိတ်ဗေဒ (Functional Analysis)တွင် ထို၂ခုအနက် အနည်းဆုံးတစ်ခုသည် တိုင်းကြောင်း အရေအတွက် (၂ခု၊ ၃ခုသာ မက) အနန္တပင် ရှိနိုင်သည့် ရပ်ဝန်းများ (infinite-dimensional spaces) လည်း သဘောတရားအားဖြင့် ဖြစ်နိုင်သည်။ [၆]
ကိုးကား
ပြင်ဆင်ရန်- ↑ Hazewinkel၊ Michiel, ed. (2001)၊ "Mapping"၊ Encyclopedia of Mathematics၊ Springer၊ ISBN 978-1-55608-010-4
- ↑ Halmos 1970
- ↑ Halmos 1970, p. 30; the words map, mapping, transformation, correspondence, and operator are often used synonymously.
- ↑ ၄.၀ ၄.၁ Berezanskii & Levitan 2012, para. 1.
- ↑ ဟု ရေးရာ၌ အကယ်၍ သည် အနန္တဒိုင်မန်းရှင်းရှိပြီး၊ သည် ဒိုင်မန်းရှင်းတစ်ခုတည်းသာ ရှိပါက (ဥပမာ ) ထိုကဲ့သို့သော ဖန်ရှင် ကို ဖန်ရှင်နယ် (functional) တစ်ခုဟုခေါ်ဆိုပြီး ဖှန်ရှင်ဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာသင်္ချာ၏ အင်္ဂလိပ်ဘာသာအမည် functional analysis ရှိ functional ဆိုသော စကားရပ်မှာ ဤဖှန်ရှင်နယ်လ်များကို ဆိုလိုခြင်းဖြစ်သည်။[၄]
- ↑ ဟု ရေးရာ၌ အကယ်၍ သည် တိုင်းကြောင်းအနန္တ ရှိပြီး၊ သည် ဒိုင်မန်းရှင်းတစ်ခုတည်းသာ ရှိပါက (ဥပမာ ) ထိုကဲ့သို့သော ဖှန်ရှင် ကို ဖှန်ရှင်နယ်လ် (functional) တစ်ခုဟုခေါ်ဆိုပြီး ဖှန်ရှင်ဆိုင်ရာ ခွဲခြမ်းစိတ်ဖြာသင်္ချာ၏ အင်္ဂလိပ်ဘာသာအမည် functional analysis ရှိ functional ဆိုသော စကားရပ်မှာ ဤဖှန်ရှင်နယ်လ်များကို ဆိုလိုခြင်းဖြစ်သည်။[၄]
| ဤ သင်္ချာနှင့် သက်ဆိုင်သော ဆောင်းပါးမှာ ဆောင်းပါးတိုတစ်ပုဒ် ဖြစ်သည်။ ဖြည့်စွက်ရေးသားခြင်းဖြင့် မြန်မာဝီကီပီးဒီးယားကို ကူညီပါ။ |



